본 글은 출처에서 발췌하여 번역한 것 임을 서두에 밝힙니다.
출처 : https://www.kdnuggets.com/2020/04/dbscan-clustering-algorithm-machine-learning.html
2022/04/04 Nagesh Singh Chauhan이 KDnuggets에 작성한 글입니다.
소개: Nagesh Singh Chauhan은 CirrusLabs의 빅데이터 개발자입니다. 통신, 분석, 영업, 데이터 과학 등 다양한 분야에서 4년 이상의 경력을 보유하고 있으며, 다양한 빅데이터 구성 요소를 전문으로 다룹니다.
DBSCAN 알고리즘과 그것을 파이썬으로 구현한 소개 내용.

2014년, DBSCAN 알고리즘은 세계 최고의 데이터 마이닝 컨퍼런스인 ACM SIGKDD에서 시간 테스트 상(이론과 실제에서 상당한 주목을 받은 알고리즘에 수여되는 상)을 수상했습니다.

소개
Cluster Analysis (군집 분석)은 데이터 포인트를 여러 개의 특정 묶음 또는 그룹으로 분리하는 비지도 학습 방법으로, 동일 그룹의 데이터 포인트는 유사한 속성을 가지지만 서로 다른 그룹의 데이터 포인트는 어떤 의미에서든 서로 다른 속성을 갖도록 합니다.
군집 분석은 다양한 거리 측정법을 기반으로 하는 여러 가지 방법으로 구성됩니다. 예를 들어, K-평균(포인트 간 거리), 친화도 전파(그래프 거리), 평균 이동(포인트 간 거리), DBSCAN(가장 가까운 포인트 간 거리), 가우시안 혼합(중심까지의 마할라노비스 거리), 스펙트럼 군집화(그래프 거리) 등이 있습니다.
모든 클러스터링 방법은 기본적으로 동일한 접근 방식을 사용합니다. 즉, 먼저 유사도를 계산한 다음 이를 사용하여 데이터 포인트를 그룹 또는 배치로 클러스터링합니다. 여기서는 노이즈가 있는 애플리케이션의 밀도 기반 공간 클러스터링(DBSCAN) 클러스터링 방법에 중점을 둘 것입니다.
클러스터링 알고리즘에 익숙하지 않다면 "K-평균 클러스터링을 사용한 이미지 분할 소개 (Introduction to Image Segmentation with K-Means clustering)"를 읽어보시기 바랍니다. "계층적 클러스터링(Hierarchical Clustering)"에 대한 문서도 참고할 수 있습니다.
K-평균 클러스터링이 이미 있는데 DBSCAN과 같은 밀도 기반 클러스터링 알고리즘이 필요한 이유는 무엇일까요?
Why do we need a Density-Based clustering algorithm like DBSCAN when we already have K-means clustering?
K-평균 클러스터링은 관련성이 낮은 관측치를 클러스터링할 수 있습니다. 모든 관측치는 벡터 공간에서 멀리 떨어져 있더라도 결국 어떤 클러스터의 일부가 됩니다. 클러스터는 클러스터 요소의 평균값에 따라 결정되므로 각 데이터 포인트는 클러스터 형성에 중요한 역할을 합니다. 데이터 포인트의 미세한 변화도 클러스터링 결과에 영향을 미칠 수 있습니다. DBSCAN에서는 클러스터 형성 방식 덕분에 이러한 문제가 크게 줄어듭니다. 특이한 형태의 데이터를 만나지 않는 한 일반적으로 큰 문제가 되지 않습니다.
k-평균의 또 다른 어려움은 k-평균을 사용하기 위해 클러스터 수("k")를 지정해야 한다는 것입니다. 대부분의 경우, 사전에 적절한 k 값이 얼마인지 알 수 없습니다.
DBSCAN의 장점은 사용하기 위해 클러스터 수를 지정할 필요가 없다는 것입니다. 필요한 것은 값 사이의 거리를 계산하는 함수와 "가까운" 거리로 간주되는 정도에 대한 지침뿐입니다. DBSCAN은 다양한 분포에서 k-평균보다 더 합리적인 결과를 생성합니다. 아래 그림은 그 사실을 보여줍니다.

밀도 기반 클러스터링 알고리즘
(Density-Based Clustering Algorithms)
밀도 기반 클러스터링은 데이터 공간에서 특정 그룹/클러스터를 식별하는 비지도 학습 방법을 의미하는데, 이는 데이터 공간에서 클러스터는 밀도가 높은 연속 영역이며, 다른 클러스터는 밀도가 낮은 연속 영역으로 구분된다는 개념을 기반으로 합니다.
잡음이 포함된 애플리케이션의 밀도 기반 공간 클러스터링(DBSCAN)은 밀도 기반 클러스터링의 기본 알고리즘입니다. 이 알고리즘은 잡음과 이상치를 포함하는 대량의 데이터에서 다양한 모양과 크기의 클러스터를 탐색할 수 있습니다.
DBSCAN 알고리즘은 두 가지 매개변수를 사용합니다.
- minPts: 클러스터링되는 최소 포인트 수(임계값), 특정 영역이 밀도가 높은 것으로 간주되기 위한 지침값.
- eps(ε): 모든 포인트의 이웃에 있는 포인트를 찾는 데 사용되는 거리 측정값.
이러한 매개변수는 밀도 도달성(Density Reachability)과 밀도 연결성(Density Connectivity)이라는 두 가지 개념을 살펴보면 이해할 수 있습니다.
밀도 측면에서 도달성(Reachability)은 한 지점이 특정 거리(eps) 내에 있을 경우 다른 지점에서 도달 가능하다는 것을 의미합니다.
반면 연결성(Connectivity)은 지점이 특정 클러스터에 있는지 여부를 판단하기 위해 전이성 기반 연결 방식(transitivity based chaining-approach)을 사용합니다. 예를 들어, p와 q 지점은 p->r->s->t->q이면 연결될 수 있습니다. (= could be connected)
(여기서 a->b 라는 표현은 b가 a 근처에 있음을 의미)
DBSCAN 클러스터링이 완료된 후에는 세 가지 유형의 지점이 있는데, 각각은 아래 그림에서 찾아볼 수 있습니다.

- Core — 거리 n 안에 최소 m개의 점을 갖는 어떤 점 (This is a point that has at least m points within distance n from itself.)
- Border — 거리 n 안에 최소 하나의 핵심 점을 갖는 어떤 점 (This is a point that has at least one Core point at a distance n.)
- Noise — 노이즈 - 코어도 경계도 아닌 점. 이 점은 거리 n안에 m개 보다도 더 적은 점만이 존재함. (This is a point that is neither a Core nor a Border. And it has less than m points within distance n from itself.)
DBSCAN 클러스터링의 알고리즘 단계 (Algorithmic steps for DBSCAN clustering)
- 알고리즘은 데이터 집합에서 임의로 한 점을 선택하여 (모든 점을 방문할 때까지) 진행합니다.
- 해당 점의 반경 'ε' 내에 최소 'minPoint'개의 점이 있으면, 이 모든 점을 동일한 클러스터에 속한 것으로 간주합니다.
- 그런 다음 각 인접 점에 대해 이웃 계산을 재귀적으로 반복하여 클러스터를 확장합니다.

매개변수 추정 (Parameter Estimation)
모든 데이터 마이닝 작업에는 매개변수 문제가 있습니다. 각 매개변수는 알고리즘에 특정한 방식으로 영향을 미칩니다. DBSCAN의 경우, 매개변수 ε와 minPts가 필요합니다.
- minPts: 경험적으로 최소 minPts는 minPts ≥ D + 1과 같이 데이터 세트의 차원 수 D에서 도출할 수 있습니다.
minPts = 1 이라는 낮은 값은 의미가 없는데, 그 이유는 각 포인트가 그 자체로 클러스터를 구성한다는 의미이기 때문입니다.
minPts ≤ 2 인 경우, 결과는 높이 ε에서 덴드로그램을 절단한 단일 링크 메트릭을 사용한 계층적 클러스터링(Hierarchical clustering)과 동일합니다. 따라서 minPts는 최소 3으로 선택해야 합니다.
그러나 일반적으로 노이즈가 있는 데이터 세트의 경우 더 큰 값이 더 좋으며, 더 중요한 클러스터를 생성합니다. 일반적으로 minPts = 2·dim을 사용할 수 있지만, 매우 큰 데이터, 노이즈가 많은 데이터 또는 중복이 많은 데이터의 경우 더 큰 값을 선택해야 할 수 있습니다. - ε: ε 값은 k-distance graph를 사용하여 선택할 수 있습니다. 이 그래프는 k = minPts-1로 가장 가까운 이웃까지의 거리를 가장 큰 값에서 가장 작은 값 순으로 표시합니다. ε 값이 적절하다는 것은 그래프에서 "팔꿈치" 모양이 나타나는 지점입니다. ε 값을 너무 작게 선택하면 데이터의 상당 부분이 클러스터링되지 않고, ε 값을 너무 크게 선택하면 클러스터가 병합되어 대부분의 객체가 동일한 클러스터에 속하게 됩니다.
일반적으로 ε 값은 작은 것이 바람직하며, 경험적으로 소수의 점만 서로 이 거리 내에 있어야 합니다. - Distance Function(거리 함수): 거리 함수의 선택은 ε 선택과 밀접하게 연관되어 있으며 결과에 큰 영향을 미칩니다. 일반적으로 매개변수 ε를 선택하기 전에 먼저 데이터 집합의 합리적인 유사도 척도를 파악해야 합니다. 이 매개변수에 대한 추정값은 없지만, 거리 함수는 데이터 집합에 맞게 적절하게 선택해야 합니다.
DBSCAN Python Implementation Using Scikit-learn
먼저 DBSCAN을 적용하여 구형 데이터를 클러스터링해 보겠습니다.
먼저 750개의 구형 학습 데이터 포인트와 해당 레이블을 생성합니다. 그 후 학습 데이터의 특징을 표준화하고 마지막으로 sklearn 라이브러리의 DBSCAN을 적용합니다.
import numpy as np
from sklearn.cluster import DBSCAN
from sklearn import metrics
from sklearn.datasets import make_blobs
from sklearn.preprocessing import StandardScaler
# Generate sample data
centers = [[1, 1], [-1, -1], [1, -1]]
X, labels_true = make_blobs(n_samples=750, centers=centers, cluster_std=0.4,
random_state=0)
X = StandardScaler().fit_transform(X)
# Compute DBSCAN
db = DBSCAN(eps=0.3, min_samples=10).fit(X)
core_samples_mask = np.zeros_like(db.labels_, dtype=bool)
core_samples_mask[db.core_sample_indices_] = True
labels = db.labels_
# Number of clusters in labels, ignoring noise if present.
n_clusters_ = len(set(labels)) - (1 if -1 in labels else 0)
n_noise_ = list(labels).count(-1)
print('Estimated number of clusters: %d' % n_clusters_)
print('Estimated number of noise points: %d' % n_noise_)
print("Homogeneity: %0.3f" % metrics.homogeneity_score(labels_true, labels))
print("Completeness: %0.3f" % metrics.completeness_score(labels_true, labels))
print("V-measure: %0.3f" % metrics.v_measure_score(labels_true, labels))
print("Adjusted Rand Index: %0.3f"
% metrics.adjusted_rand_score(labels_true, labels))
print("Adjusted Mutual Information: %0.3f"
% metrics.adjusted_mutual_info_score(labels_true, labels))
print("Silhouette Coefficient: %0.3f"
% metrics.silhouette_score(X, labels))
# Plot result
import matplotlib.pyplot as plt
%matplotlib inline
# Black removed and is used for noise instead.
unique_labels = set(labels)
colors = [plt.cm.Spectral(each)
for each in np.linspace(0, 1, len(unique_labels))]
for k, col in zip(unique_labels, colors):
if k == -1:
# Black used for noise.
col = [0, 0, 0, 1]
class_member_mask = (labels == k)
xy = X[class_member_mask & core_samples_mask]
plt.plot(xy[:, 0], xy[:, 1], 'o', markerfacecolor=tuple(col),
markeredgecolor='k', markersize=14)
xy = X[class_member_mask & ~core_samples_mask]
plt.plot(xy[:, 0], xy[:, 1], 'o', markerfacecolor=tuple(col),
markeredgecolor='k', markersize=6)
plt.title('Estimated number of clusters: %d' % n_clusters_)
plt.show()DBSCAN_sklearn_implementation.py

검은색 데이터 점은 위 결과에서 이상치를 나타냅니다. 다음으로, DBSCAN을 적용하여 비구형 데이터를 클러스터링합니다.
import numpy as np
import matplotlib.pyplot as plt
from sklearn import metrics
from sklearn.datasets import make_circles
from sklearn.preprocessing import StandardScaler
from sklearn.cluster import DBSCAN
X, y = make_circles(n_samples=750, factor=0.3, noise=0.1)
X = StandardScaler().fit_transform(X)
y_pred = DBSCAN(eps=0.3, min_samples=10).fit_predict(X)
plt.scatter(X[:,0], X[:,1], c=y_pred)
print('Number of clusters: {}'.format(len(set(y_pred[np.where(y_pred != -1)]))))
print('Homogeneity: {}'.format(metrics.homogeneity_score(y, y_pred)))
print('Completeness: {}'.format(metrics.completeness_score(y, y_pred)))
print("V-measure: %0.3f" % metrics.v_measure_score(labels_true, labels))
print("Adjusted Rand Index: %0.3f"
% metrics.adjusted_rand_score(labels_true, labels))
print("Adjusted Mutual Information: %0.3f"
% metrics.adjusted_mutual_info_score(labels_true, labels))
print("Silhouette Coefficient: %0.3f"
% metrics.silhouette_score(X, labels))DBSCAN_non_spherical_data.py

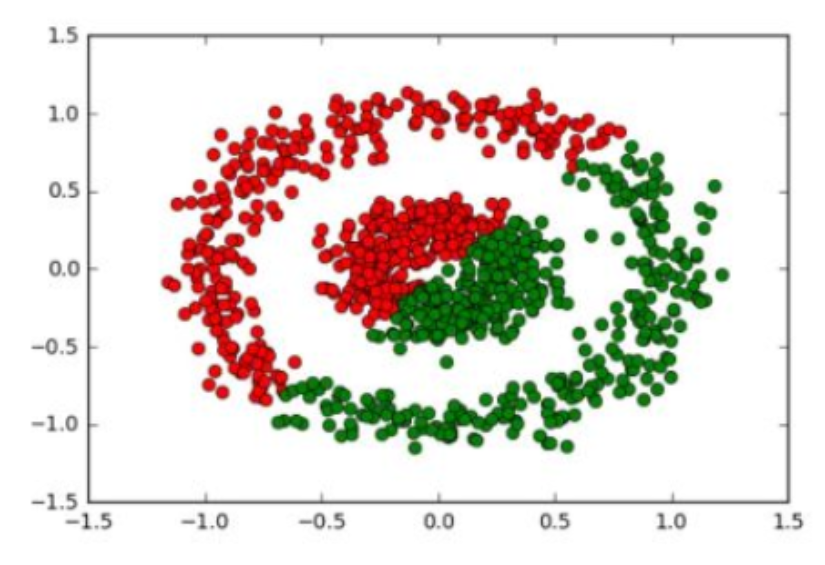
완벽합니다.
같은 데이터셋으로 K-means와 비교를 해볼까요?
K-means는 다음과 같이 완전히 잘못된 결과가 나옵니다.
DBSCAN 알고리즘 복잡도 (The Complexity of DBSCAN)
알고리즘을 얘기할 때 빠질 수 없는게 있습니다. 바로 알고리즘의 복잡도죠.
알고리즘이 아무리 훌륭한 결과를 낸다하더라도 복잡도가 너무 높으면(= 계산이 너무 오래걸리면) 사용할 수가 없죠. 예를들어 어떤 엄청난 알고리즘이 있는데, 계산결과가 10만년 뒤에 나온다면, 그 알고리즘을 사용할 수는 없을거에요.
- Best Case : 인덱싱 시스템을 사용하여 데이터 세트를 저장하고 이웃 쿼리가 로그 시간 내에 실행되는 경우, 평균 실행 시간 복잡도는 O(nlogn)입니다.
- Worst Case: 인덱스 구조를 사용하지 않거나 축퇴된 데이터(예: ε보다 작은 거리 내에 있는 모든 점)의 경우, 최악의 실행 시간 복잡도는 O(n²)입니다.
- Average Case: 데이터 및 알고리즘 구현에 따라 최상의 경우/최악의 경우와 동일합니다.
결론 (Conclusion)
밀도 기반 클러스터링 알고리즘은 임의의 형태의 클러스터를 학습할 수 있으며, 레벨 셋 트리 알고리즘을 사용하면 밀도 차이가 큰 데이터셋에서 클러스터를 학습할 수 있습니다.
하지만 이러한 알고리즘은 K-Means와 같은 매개변수 클러스터링 알고리즘에 비해 조정이 다소 어렵다는 점을 지적하고 싶습니다. DBSCAN이나 Level Set Tree의 엡실론(ε)과 같은 매개변수는 K-Means의 클러스터 수 매개변수에 비해 추론하기가 직관적이지 않기 때문에 이러한 알고리즘에 적합한 초기 매개변수 값을 선택하기가 더 어렵습니다.
이 글은 여기까지입니다. 즐겁게 읽으셨기를 바라며, (여기 말고 원본글에) 제안/의견/질문은 댓글로 남겨주세요.
(물론 여기에 남기는 것도 환영합니다)
Thanks for Reading!
참고 문헌
https://www.kdnuggets.com/2020/04/dbscan-clustering-algorithm-machine-learning.html
https://www.stratio.com/blog/graph-database-clustering-solution/
https://github.com/NSHipster/DBSCAN
https://www.digitalvidya.com/blog/the-top-5-clustering-algorithms-data-scientists-should-know/
https://en.wikipedia.org/wiki/Hierarchical_clustering
'개발자의 기록 노트 > Algorithm' 카테고리의 다른 글
| [보안] 암호화 알고리즘 (0) | 2012.07.18 |
|---|---|
| 10진수를 2진수로 변환하는 알고리즘 (또다른 방법) (4) | 2011.07.22 |
| 해시 테이블에 대하여 (about Hash Table) (0) | 2011.06.11 |
| OAuth 인증방식 이해하기 (0) | 2011.04.16 |
| Travelling Salesman Problem Portal Site (0) | 2011.04.13 |